Kinetic Energy Operator: Physics का सबसे महत्वपूर्ण उपकरण!

Kinetic Energy Operator के बारे में समझना जरूरी है, खासकर अगर आप Physics या Quantum Mechanics जैसे विषयों में रुचि रखते हैं। Kinetic Energy Operator एक ऐसा गणितीय उपकरण है जो किसी भी सिस्टम की गतिज ऊर्जा की गणना करने में मदद करता है। यह Quantum Mechanics का एक महत्वपूर्ण हिस्सा है, जहाँ कणों की गतिज ऊर्जा को सटीक रूप से मापा और समझा जाता है।

जब हम किसी कण की गति और उसके द्रव्यमान की बात करते हैं, तो Kinetic Energy Operator एक ऐसी विधि प्रदान करता है जिससे हम यह जान सकते हैं कि किसी कण की ऊर्जा किस तरह काम करती है। इसका उपयोग कणों के व्यवहार को समझने के लिए किया जाता है, खासकर जब वे बहुत छोटे पैमाने पर होते हैं, जैसे कि इलेक्ट्रॉन्स या क्वार्क्स।

इस ब्लॉग पोस्ट में, हम आपको विस्तार से बताएंगे कि गतिज ऊर्जा परिचालक कैसे काम करता है, इसके प्रमुख गुण क्या हैं और इसे Physics में क्यों इतना महत्वपूर्ण माना जाता है। अगर आप Quantum Physics के बारे में और जानने की इच्छा रखते हैं, तो यह जानकारी आपके लिए बेहद उपयोगी होगी।

क्वांटम यांत्रिकी और गति ऊर्जा (Kinetic Energy) के जटिल सिद्धांतों को समझने के लिए गहराई में जाना आवश्यक है। यह लेख “Kinetic Energy Operator” की परिभाषा, उसके विभिन्न प्रकार, और क्वांटम सिस्टम में इसके उपयोग के बारे में विस्तृत जानकारी प्रदान करेगा। इससे आपको इस ऑपरेटर की भूमिका को समझने में मदद मिलेगी, जो कणों की गतिज ऊर्जा को व्यक्त करता है और यह क्वांटम यांत्रिकी में क्यों आवश्यक है।

Kinetic Energy Operator क्या है?

सरल भाषा में कहें, तो Kinetic Energy Operator वह गणितीय उपकरण है, जिसका उपयोग क्वांटम यांत्रिकी में कणों की गतिज ऊर्जा को व्यक्त करने के लिए किया जाता है। यह ऑपरेटर कणों की गति और उनके ऊर्जा स्तरों का गणितीय रूप से वर्णन करता है।

शास्त्रीय यांत्रिकी में, गति ऊर्जा को समझना अपेक्षाकृत आसान है। यह कण के द्रव्यमान और गति के गुणनफल का आधा होता है, जिसे हम आमतौर पर 12mv2\frac{1}{2} mv^221​mv2 के रूप में जानते हैं। लेकिन क्वांटम यांत्रिकी में चीजें जटिल हो जाती हैं, क्योंकि कणों के व्यवहार को तरंग फलन (Ψ\PsiΨ) के माध्यम से व्यक्त किया जाता है, और Kinetic Energy Operator का उपयोग इन तरंग फलनों पर किया जाता है।

गतिज ऊर्जा परिचालक का गणितीय रूप

Kinetic Energy Operator का गणितीय निरूपण इस प्रकार है:

T^=−ℏ22m∇2\hat{T} = -\frac{\hbar^2}{2m} \nabla^2T^=−2mℏ2​∇2

यहां, ℏ\hbarℏ (reduced Planck’s constant), mmm (कण का द्रव्यमान), और ∇2\nabla^2∇2 (लैप्लासियन ऑपरेटर) हैं। इस समीकरण का उपयोग स्वतंत्र कणों की गतिज ऊर्जा की गणना के लिए किया जाता है। यह क्वांटम यांत्रिकी में कणों की ऊर्जा का एक मूलभूत उपकरण है।

Types of Kinetic Energy Operator

Kinetic Energy Operator को विभिन्न स्थितियों और प्रणालियों के आधार पर कई श्रेणियों में बांटा जा सकता है। यहाँ मुख्य चार प्रकार के ऑपरेटरों का विवरण दिया गया है:

1. Classical गतिज ऊर्जा परिचालक:

• शास्त्रीय यांत्रिकी में गति ऊर्जा 12mv2\frac{1}{2} mv^221​mv2 के रूप में व्यक्त की जाती है, जहाँ mmm कण का द्रव्यमान है और vvv उसकी गति। यह फॉर्मुला सरल और प्रत्यक्ष है, और इसका उपयोग पारंपरिक भौतिकी में किया जाता है।
• उदाहरण: जब हम एक चलती हुई कार या एक गिरते हुए पत्थर की गति और ऊर्जा का विश्लेषण करते हैं, तो हम इस शास्त्रीय ऑपरेटर का उपयोग करते हैं।

2. Quantum गतिज ऊर्जा परिचालक:

• क्वांटम यांत्रिकी में, गतिज ऊर्जा परिचालक कणों की गति और ऊर्जा को गणितीय रूप से व्यक्त करता है। यह ऑपरेटर तरंग फलन Ψ\PsiΨ पर लागू होता है और इसका उपयोग कणों की आंशिक अवकल समीकरणों के रूप में किया जाता है।
• उदाहरण: इलेक्ट्रॉनों के व्यवहार का विश्लेषण करने के लिए, जब वे परमाणु के चारों ओर घूमते हैं, तो इस ऑपरेटर का उपयोग किया जाता है।
• इस प्रकार के ऑपरेटर के उपयोग से कणों की गतिज ऊर्जा और तरंग फलन के बीच संबंध का अध्ययन किया जाता है।

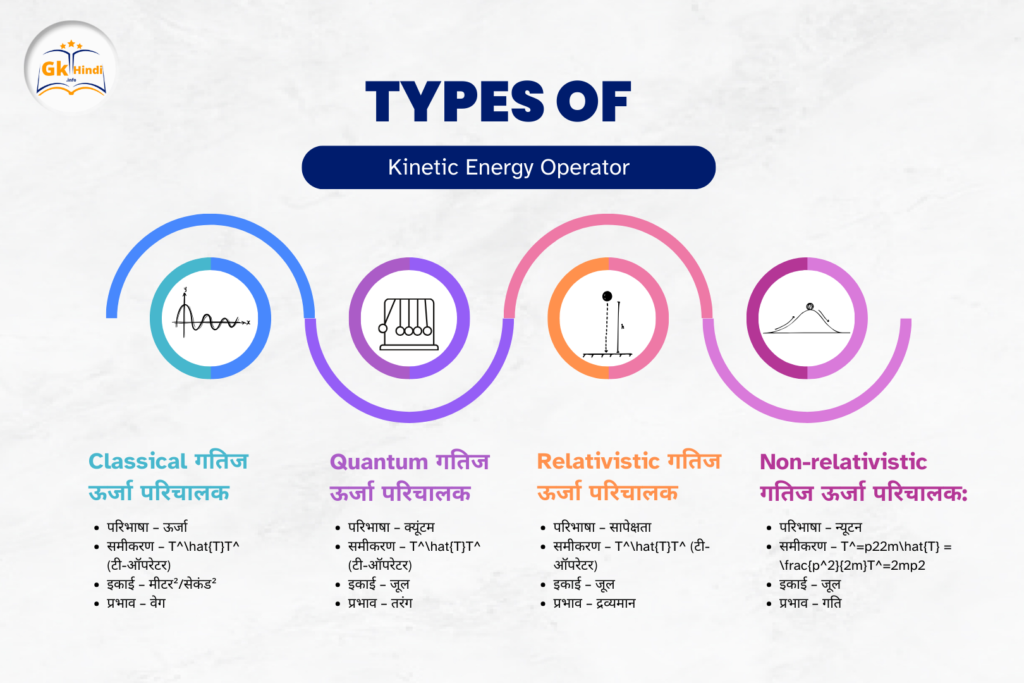
3. Relativistic गतिज ऊर्जा परिचालक:

• जब कणों की गति प्रकाश की गति के करीब होती है, तो इस ऑपरेटर का उपयोग किया जाता है। इस प्रकार का ऑपरेटर विशिष्ट है क्योंकि इसमें सामान्य गति के सिद्धांत की तुलना में अधिक जटिलता होती है।
• इस ऑपरेटर का निरूपण Einstein की सापेक्षता के सिद्धांत पर आधारित होता है, और इसका उपयोग मुख्य रूप से उन स्थितियों में किया जाता है जहां गति बहुत तेज़ हो, जैसे उप-परमाणु कणों के व्यवहार में।
• उदाहरण: उच्च गति वाले कणों का विश्लेषण करते समय, जैसे कि CERN में होने वाले कणों के टकराव में, इस ऑपरेटर का उपयोग किया जाता है।

4. Non-relativistic गतिज ऊर्जा परिचालक:

• यह ऑपरेटर उन स्थितियों में लागू होता है जहाँ कणों की गति अपेक्षाकृत धीमी होती है और यह सापेक्षता के सिद्धांत पर आधारित नहीं होता।
• इसे रोज़मर्रा की क्वांटम यांत्रिकी में अधिकतर मामलों में उपयोग किया जाता है, जैसे कि इलेक्ट्रॉन और प्रोटॉन जैसी कणों का अध्ययन करते समय।
• उदाहरण: जब हम हाइड्रोजन परमाणु के इलेक्ट्रॉन की ऊर्जा का विश्लेषण करते हैं, तब इस ऑपरेटर का उपयोग होता है।

Schrödinger समीकरण में गतिज ऊर्जा परिचालक की भूमिका

Schrödinger समीकरण क्वांटम यांत्रिकी में एक महत्वपूर्ण भूमिका निभाता है, और इसके माध्यम से हम किसी सिस्टम की कुल ऊर्जा का विश्लेषण कर सकते हैं। Schrödinger समीकरण को निम्नलिखित रूप में व्यक्त किया जा सकता है:

HΨ=EΨH \Psi = E \PsiHΨ=EΨ

यहाँ HHH Hamiltonian है, जो सिस्टम की कुल ऊर्जा को दर्शाता है। इस समीकरण में, Kinetic Energy Operator (TTT) गति ऊर्जा का प्रतिनिधित्व करता है, और इसे संभावित ऊर्जा (VVV) के साथ जोड़ा जाता है। यह समीकरण कणों के ऊर्जा स्तरों का निर्धारण करता है, और इसके माध्यम से हम कण की गति और ऊर्जा के संबंध का विश्लेषण कर सकते हैं।

Eigenstates और Eigenvalues की अवधारणा

Eigenstates और Eigenvalues Kinetic Energy Operator के संदर्भ में विशेष रूप से महत्वपूर्ण हैं।

1. Eigenvalues

ये गति ऊर्जा के विशिष्ट मान होते हैं, जो Kinetic Energy Operator द्वारा प्राप्त किए जाते हैं। इन्हें कणों की गतिज ऊर्जा के मान के रूप में जाना जाता है।

2. Eigenstates

ये कणों की तरंग फलन होते हैं, जो ऑपरेटर के साथ स्थिर रहते हैं। जब किसी सिस्टम को Eigenstates और Eigenvalues में विभाजित किया जाता है, तो यह सिस्टम की ऊर्जा और तरंग फलन के व्यवहार का विश्लेषण करने में सहायक होता है।

Physics GK Question In Hindi: Physics के सामान्य ज्ञान से जुड़े सवाल प्रतियोगी परीक्षाओं के लिए महत्वपूर्ण होते हैं। यहां आप Physics GK Question In Hindi के जरिए फिजिक्स के महत्वपूर्ण कॉन्सेप्ट्स को आसानी से समझ सकते हैं।

हेमिल्टोनियन और गतिज ऊर्जा परिचालक का संबंध

Hamiltonian (HHH) ऑपरेटर क्वांटम सिस्टम की कुल ऊर्जा को व्यक्त करता है, जिसमें Kinetic Energy Operator (TTT) और Potential Energy Operator (VVV) दोनों शामिल होते हैं। यह ऑपरेटर क्वांटम सिस्टम की गति और ऊर्जा का गहन विश्लेषण करने के लिए उपयोग किया जाता है। Hamiltonian का उपयोग करते हुए, हम किसी भी क्वांटम सिस्टम में कणों के ऊर्जा स्तरों का निर्धारण कर सकते हैं।

विभिन्न Coordinate Systems में Kinetic Energy Operator

Kinetic Energy Operator का उपयोग विभिन्न coordinate systems में किया जा सकता है:

1. Cartesian Coordinates: यहाँ यह सबसे सरल रूप में कार्य करता है। इसका उपयोग तब किया जाता है जब सिस्टम की समरूपता सीधे X, Y, और Z अक्षों के साथ हो।
2. Spherical Coordinates: जब कण उप-परमाणु स्तर पर होते हैं, तो यह ऑपरेटर गोल निर्देशांकों में अधिक जटिल रूप में कार्य करता है। इसका उपयोग परमाणु और उप-परमाणु कणों के अध्ययन में किया जाता है।
3. Cylindrical Coordinates: सिलेंड्रिकल समरूपता वाले सिस्टम के लिए, यह ऑपरेटर उपयुक्त होता है। इसे तब उपयोग किया जाता है जब सिस्टम की समरूपता सिलेंड्रिकल संरचना में हो।

वास्तविक जीवन में गतिज ऊर्जा परिचालक का उपयोग

गतिज ऊर्जा परिचालक का उपयोग कई क्षेत्रों में किया जाता है, जैसे:

गतिज ऊर्जा परिचालक और अन्य ऑपरेटरों के बीच संबंध

Kinetic Energy Operator का अन्य ऑपरेटरों के साथ निकट संबंध है:

FAQ Of Kinetic Energy Operator

Conclusion Of Kinetic Energy Operato

“Kinetic Energy Operator” क्वांटम यांत्रिकी और भौतिकी में एक महत्वपूर्ण उपकरण है, जो कणों की गतिज ऊर्जा का वर्णन करने में सहायता करता है। इसके विभिन्न प्रकार और अनुप्रयोग भौतिकी के विभिन्न क्षेत्रों में विस्तृत रूप से उपयोग किए जाते हैं। Kinetic Energy Operator का भविष्य के शोध और अध्ययन में और अधिक महत्वपूर्ण भूमिका हो सकती है, जिससे भौतिकी और ऊर्जा के जटिल सिद्धांतों को और बेहतर ढंग से समझा जा सके।